A la recherche du cours parfait
- Nov 27, 2017
- 5 min read

En formation, j'aime bien, quand je peux, envoyer des petits films à visionner et enchaîner sur un QCM. Bref, de la formation inversée classique. Sauf que mes QCM sont plus des supports pour des débats lors de la formation. C'est ainsi que la question ci-contre me permet de discuter du sens de "évaluation" et de "acquise".
La dernière fois cependant, lorsque j'ai présenté cette capture d'écran, une stagiaire a réagi assez violemment. Elle avait manifestement répondu la mauvaise réponse et cela était difficile pour elle compte tenu de son passé de bonne élève. Naturellement pour moi, pas de bonne ou de mauvaise réponse, juste un support pour parler du fond. Là, il n'a pas été possible de discuter du fond, elle entraînait systématiquement la discussion sur "Comment aurait-on dû changer la question pour ne pas induire les gens en erreur ?".

Il était important pour elle de faire des questions, des énoncés où tout soit clair. Que l'élève ne se trompe pas. On retrouve ici une croyance décrite dans le livre d'Astolfi [1]: "L’idée n’est-elle pas que si le professeur explique bien, s’il veille au bon rythme, s’il choisit aussi les bons exemples et si, bien sûr, les élèves sont pour leur part attentifs et motivés, il ne devrait – normalement – survenir aucune erreur ?"
Pour ma stagiaire, attentive et motivée, s'il y avait erreur, c'est que moi, formatrice, je n'avais pas bien fait mon travail.
Quelque part se cache, tapi dans l'ombre, le mythe du "cours parfait". Ce cours tellement clair et précis qu'il n'induit aucune erreur, tous les élèves seraient capables de le comprendre parfaitement, du premier coup. On connait tous des collègues qui passent une bonne partie de leur carrière à la recherche de ce "cours mythique", retouchant la structure, les mots et parfois même la ponctuation de leur cours "parce qu'ils n'ont pas compris ça cette année". On retrouve ça en formation initiale, une bonne partie de la formation consiste à apprendre "à faire un cours". Que dire de la prédominance des fiches de préparation au primaire...

On retrouve ça également de "l'autre côté" : les élèves veulent des cours où ils sortent en se disant "j'ai compris". Un bon cours, c'est un cours qu'on comprend.
Sauf que...
Le premier problème, c'est qu'un cours limpide peut donner une fausse impression de maîtrise. Je n'ai pas (encore) de données bibliographique (je sais qu'elles existent mais il faudra être un peu patient) alors je vais faire appel au vécu pour faire comprendre cette notion. La fausse impression de maîtrise, c'est l'élève "studieuse" qui vient vous voir avec son contrôle marqué 10 et qui vous dit "pourtant j'avais tout lu, tout appris, j'avais tout compris". Personnellement, cette histoire m'est arrivée en 1ereS. J'étais élève, pas vraiment studieuse et j'ai écouté d'un coin de l'oreille le chapitre sur les barycentres. Je n'ai jamais vu le problème, jamais vu de difficulté. Du coup, je ne me suis jamais frottée aux exercices puisque "j'avais compris". Un 3,5/20 (on s'en souvient hein, de ses mauvaises notes) m'a appris une fois pour toute que écouter et comprendre ne suffisait pas pour maîtriser.
La fausse impression de maîtrise peut aussi se faire dans la durée. Lorsqu'on prépare un examen en mode "massé" (ce qui s'appelle en langage courant "bachoter") on a compris le jour de l'examen. Mais 1 mois, 2 mois, 1 an après, qu'avons-nous retenu ? La vraie maîtrise n'est-elle pas celle qui dure dans le temps ?
L'autre problème, c'est que pour rendre nos cours limpides, on a tendance à "découper" les notions. On obtient ainsi des petits morceaux que l'élève peut comprendre facilement. On enseigne chaque petit morceau et on pense ainsi que la notion en entier est passée. Or, Edgar Morin [2], travailleur de la pensée complexe nous dit bien que "le tout est à la fois plus et moins que la somme des parties". Donc enseigner la somme des parties, ce n'est pas enseigner le tout.
J'ai également expérimenté cela en tant qu'élève. Maths spé cette fois-ci, année des concours, j'avais le meilleur professeur de chimie du lycée (c'est bien grâce à lui que j'ai fait des études de chimie après). Cours sur la thermodynamique chimique. Pour ceux qui ne connaissent pas la thermodynamique chimique (comment ça vous êtes nombreux ?) c'est une matière assez complexe avec beaucoup de grandeurs physiques, de modèles différents et d'équations dans tous les sens (en voici un extrait en image pour le plaisir).
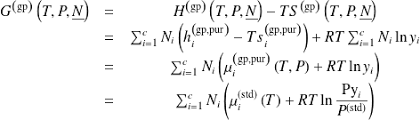
Il avait imaginé une progression pédagogique très progressive, modèle par modèle. Il s'approchait vraiment du fameux "cours parfait". Sur une matière ardue, je n'ai jamais eu l'impression de ne pas comprendre le cours. A chaque moment du cours, je me disais "oui, c'est évident, c'est clair". On peut dire que j'avais compris. Et pourtant, au moment de réviser le contrôle et surtout les concours plusieurs mois après, je n'arrivais plus très bien à me souvenir des grands concepts. Les petits morceaux étaient acquis mais je n'avais pas réussi à acquérir le concept général. Ce n'est que beaucoup d'années plus tard, en révisant l'agrégation, en me plongeant dans la thermodynamique et en me disant "mais je n'y comprends rien !" que j'ai enfin réussi à appréhender les concepts derrière cette liste d'équations.
Cette intuition que j'ai eu en tant qu'élève est étayée aujourd'hui par la recherche en sciences cognitives. Rendre une tâche plus difficile peut conduire à un meilleur apprentissage et une mémorisation plus durable. C'est le terme de "difficultés souhaitables" introduit par R.A. Bjork & E. L. Bjork [3] en 1992. Cela peut paraître paradoxal. Et pourtant, on retient plus facilement un texte écrit avec une typographie inhabituelle ou avec des blancs. L'effort consacré à lire le texte joue un rôle sur la mémorisation de ce texte [4].
Voici donc un petit résumé d'une étude illustrant ceci [5]. Toujours dans les années 1990, une équipe de baseball (hey, c'est une étude américaine) a participé à une expérience sur les performances à la batte. Toute l'équipe a participé à 2 entraînements hebdomadaires supplémentaires qui consistaient en 45 lancers. La moitié de l'équipe s'est entraîné de manière standard : 15 balles rapides puis 15 balles courbes puis 15 balles avec changement de vitesse. Pour la deuxième moitié de l'équipe, l'entraînement était plus difficile : les 3 types de lancés étaient mélangés aléatoirement ce qui fait que le batteur ne savait jamais quel type de balle allait lui arriver dessus. Au bout de 6 semaines de ce régime, ceux du premier groupes ont déclarés se sentir "à l'aise"tandis que ceux du deuxième groupe ont rapporté un entraînement douloureux. Bref, si cela avait été des élèves, ils auraient trouvé le cours "moins bon" parce qu'ils n'auraient "pas compris" (du moins du premier coup). En revanche, lorsque les performances des joueurs ont été mesurées, les deux groupes avaient progressé mais ceux du deuxième groupe nettement plus. Il n'y a donc pas de corrélation entre l'impression des apprenants par rapport à l'apprentissage et la performance finale des apprenants.
Cela paraît paradoxal... Et pourtant cela correspond à mon vécu. Mes élèves sortent rarement contents de mon cours "on ne comprends rien, c'est compliqué". C'est difficile à gérer et pourtant les choses s'arrangent d'elle-même lorsqu'ils se rendent compte qu'au final, ils apprennent mieux. Et c'est bien ça le plus important.
Mais alors, comment expliquer ce paradoxe ? Qu'apportent les difficultés aux élèves lors de l'apprentissage ? C'est ce que je vous propose de voir la semaine prochaine.
[2] Edgar Morin, MOOC connaître et agir en complexité, Coursera
[3] R. A. Bjork & E. L. Bjork, A new theory of disuse and an old theory of stimulus fluctuation, in A. F. Healy, S. M. Kosslyn & R. M. Shiffrin (eds.), From learning processes to cognitive processes : Essays in honor of William K. Estes, vol. 2, p. 35-67 (Hillsdale, NJ : Erlbaum, 1992)
[4] M. A. McDaniel, G. O. Einstein, P. K. Dunay & R. Cobb, Encoding difficulty and memory : Toward a unifying theory, Journal of Memory and Langage 25 (1986) p. 645-656
[5] K. G. Halls, D. A. Domingues & R. Cavazos, Contextual interferences effects with skilled baseball players, Perceptual and Motor Skills 78 (1994), p. 835-841


























Comments